Guidance Algorithm: Left or Right Side of the Line

I was working on a very interesting (and frustrating) algorithm recently at work that really messed with my head. After I had it solved and behind me, I decided to put it into prose and post it here – just in case my future self needs a reminder of how it works. Hope you find it useful too!

Updated 2020-Dec-29 with:

• A working Jupyter Notebook here that shows this algorithm implemented in Python3.
• Tweaks to the algorithm description below.

Problem Statement

Given an arbitrary line on the surface of an ellipsoid with known start and end points (implying directionality); and given an arbitrary point that is not on the line (known within some reasonably small tolerance that is « the line length); determine which side (e.g. LEFT or RIGHT) of the line the point lies on.

Quick sketch of our geometry:

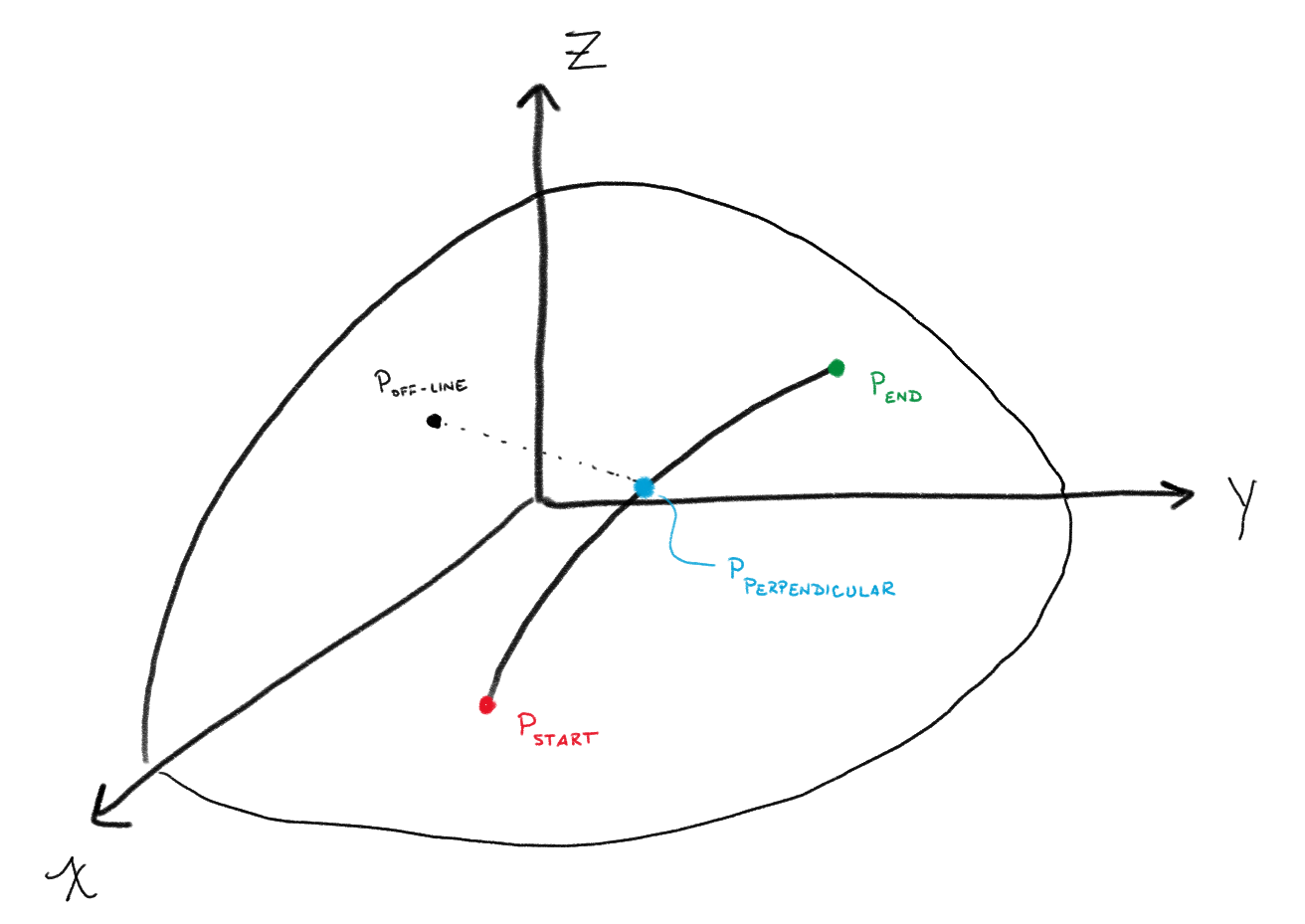
Background

This exact problem occurs routinely in automated path-following guidance algorithms that build their paths on the earth surface. Vehicles like drones, airplanes, robots and the like all need to follow a path from their current location to their destination. And that path is usually “on the ground”. The vehicle will rarely be exactly “on the path” in a mathematical sense. Sure, it should know where it is (GPS being so helpful). But, what should it do to get from where it is to closer to the path? The obvious question to answer before determining a control response is: on which side of path is the vehicle? To the left or the right?

Solution

In a flat-earth Euclidean world, this problem is easily solved using vector cross-products. To me, the challenge occurred (mentally) once I defined the line as being a geodesic on an ellipsoid.

Turns out it’s not that hard. You still use a cross-product. Vector-calc win, peeps!

Here we go. (Use the diagram above as reference.)

Solve for the course, $course_\text{at start point}$ of the line at the start point, $P_\text{start}$. Let this be defined in the NED Frame.

Solve for a point $P_\text{closest-point-on-line}$ that lies on the line and that represents a perpendicular projection from point $P_\text{off-line}$ to the line.

Let there be a vector $\vec{C}$ that is in the ECEF Frame and points to the point $P_\text{off-line}$.

Let there be a vector $\vec{D}$ that is in the ECEF Frame and points to the point $P_\text{closest-point-on-line}$.

Take the cross-product of the two vectors to determine a new vector $V$ that is orthogonal to $P_\text{closest-point-on-line}$ and $P_\text{off-line}$.

\[\vec{V} = \vec{C} \times \vec{D}\]

The components of $\vec{V}$ contain the information for our solution. We can examine the signs of the terms in $\vec{V}$ and determine on which side of our line $P_\text{off-line}$ exists.

If we constrain our solution space to being for lines on the continent of North America, the algorithm looks like this:

if $course_\text{at start point}$ is approximately 90 degrees:
    $V_x is positive, ON_LEFT_SIDE$
    $V_x is negative, ON_RIGHT_SIDE$

if $course_\text{at start point}$ is approximately 270 degrees:
    $V_x is negative, ON_RIGHT_SIDE$
    $V_x is positive, ON_LEFT_SIDE$

if $course_\text{at start point}$ has a northly component:
    $V_z is positive, ON_LEFT_SIDE$
    $V_z is negative, ON_RIGHT_SIDE$

if $course_\text{at start point}$ has a southerly component:
    $V_z is negative, ON_LEFT_SIDE$
    $V_z is positive, ON_RIGHT_SIDE$

Of course, I constrained my solution to a particular region of the globe. But, if you’re thinking about the geometry here, you’ll find a way to use the components of $\vec{V}$ and expand this into a more general, global solution.

Do you have a better way to solve this? Let me know by starting a GitHub Discussion!

When I get the chance, I’ll post an implementation of this in a Jupyter Notebook. (Done! Take a look)